MIT 6.006 Notes | Insertion Sort & Merge Sort

Posted on | | Visitors

最近在学习 MIT 的算法课：Introduction to Algorihtms
地址在这里，打算对着《CLRS》把这门课跟完
顺手写一些笔记，放在这里，以供日后复习查阅

这一篇文章对应的是6.006中 Lecture 3 的内容
包括了 Insertion Sort & Merge Sort
下面就来一一分析

Insertion Sort

For i = 1, 2, …., n
    Insert A[i] into sorted array A[0 : n - 1]
    by pairwise swaps down to the correct position

Insertion Sort
Image Source:
http://interactivepython.org/courselib/static/pythonds/SortSearch/TheInsertionSort.html

这里要向大家推荐一个很好用的算法可视化网站：https://visualgo.net/en
里面有常用的数据结构和算法，并以动画的形式展现出来

对于 Insertion Sort，这里给出了它的伪代码

1
2
3
4
5
6
repeat (numOfElements - 1) times
  set the first unsorted element as the minimum
  for each of the unsorted elements
    if element < currentMinimum
      set element as new minimum
  swap minimum with first unsorted position

Java 实现如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public class InsertionSort{
    public static void sort(int[] array){
        int len = array.length;
        for (int i = 1; i < len; i++){
            int key = array[i];
            int j = i - 1;
            while (j >= 0 && array[j] > key){
                array[j + 1] = array[j];
                j = j - 1;
            }
            array[j + 1] = key;
        }
    }
    public static void main(String[] args){
        int[] array = {12, 11, 13, 5, 6};
        sort(array);
        for (int i = 0; i < array.length; i++){
            System.out.print(array[i] + " ");
        }
        System.out.println();
    }
}

下面来稍微分析一下这个算法
我们从 array 的第二项开始，即把 array1 当成 key
一直遍历到 array[n - 1]，一共有 n - 1 项, 即θ(n)
对每一项来说，最坏情况是它比前面已经 sort 好了的 element 都要小
即与前面的每一项都要进行 compare & swap，也为 θ(n)
时间复杂为 O(n^2)

注意上面我们所说的这个步骤：compare & swap, 如果 compare
的时间花费远大于 swap
那么我们要思考有没有一种方式来减少 compare 的时间花费？
答案是 binary search，对于每个 key，在前面已经 sorted 的 array 里用 binary search
这样可以把时间复杂度降为 O(nlgn)

注意这里所说的 O(nlgn) 是对 compare 来说的
swap 仍然花费 O(n^2), 因为在数组这种数据结构里，元素是相邻的

Merge Sort

Merge Sort 体现了 Divide & Conqure 的思想

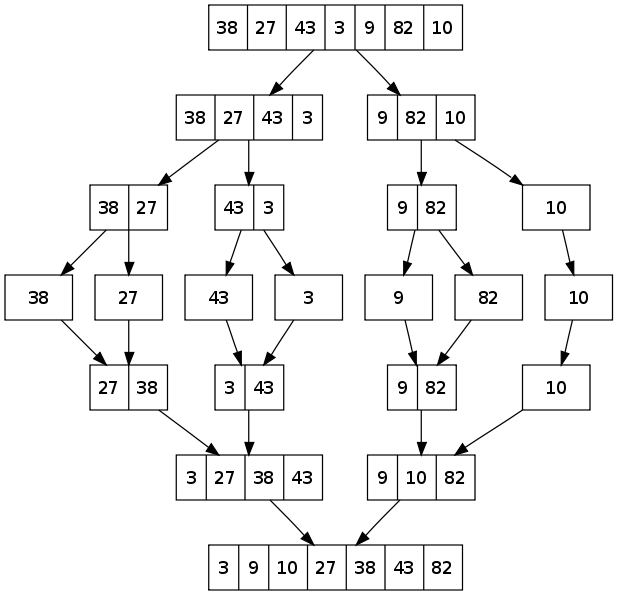
Merge Sort
Image Source: http://www.geeksforgeeks.org/merge-sort/

Merge Sort 可视化演示：https://visualgo.net/en/sorting

Merge Sort 的伪代码：

1
2
3
4
5
6
7
8
9
10
MergeSort(arr[], l,  r)
If r > l
     1. Find the middle point to divide the array into two halves:  
             middle m = (l+r)/2
     2. Call mergeSort for first half:   
             Call mergeSort(arr, l, m)
     3. Call mergeSort for second half:
             Call mergeSort(arr, m+1, r)
     4. Merge the two halves sorted in step 2 and 3:
             Call merge(arr, l, m, r)

Java 代码实现如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
public class MergeSort{
    void merge(int[] array, int l, int m, int r){
        // Find size of wo subarrays to be merged
        int leftLength = m -  l + 1;
        int rightLength = r - m;
        // Create temp arrays
        int L[] = new int[leftLength];
        int R[] = new int[rightLength];
        // Copy data to temp arrays
        for (int i = 0; i < leftLength; i++){
            L[i] = array[l + i];
        }
        for (int i = 0; i < rightLength; i++){
            R[i] = array[m + 1 + i];
        }
        // Initial indexes od first and second subarrays
        int i = 0, j = 0;
        // Initial index of merged subarray array
        int k = l;
        while (i < leftLength && j < rightLength){
            if (L[i] <= R[j]){
                array[k] = L[i];
                i++;
            }
            else{
                array[k] = R[j];
                j++;
            }
            k++;
        }
        // Copy remaining elements of L[] or R[] if any
        while (i < leftLength){
            array[k] = L[i];
            k++;
            i++;
        }
        while (j < rightLength){
            array[k] = R[j];
            k++;
            j++;
        }
    }
    // Main function that sorts array[l : r] using merge()
    void sort(int[] array, int l, int r){
        if (l < r){
            int m = (l + r) / 2;
            sort(array, l, m);
            sort(array, m + 1, r);
            merge(array, l, m, r);
        }
    }
    static void printArray(int[] array){
        for (int i = 0; i < array.length; i++){
            System.out.print(array[i] + " ");
        }
        System.out.println();
    }
    public static void main(String[] args){
        int[] array = {12, 11, 13, 5, 6, 7};
        System.out.println("Given array:");
        printArray(array);
        MergeSort m = new MergeSort();
        m.sort(array, 0, array.length - 1);
        System.out.println("Sorted array: ");
        printArray(array);
    }
}

下面我们来分析一下这个代码，把关注点放在时间和空间的话费上

首先我们可以根据整个流程分析出以下式子：T(n) = C1 + T(n/2) + cn
C1 is Divide time, cn is Merge time

Merge sort
Image Source: https://www2.hawaii.edu/~janst/311/Notes/Topic-02.html
对这个树来说，高度为 1 + lgn, 一共有 n leaves
每一层花费的时间都是 cn
所以总时间是 T(n) = (1 + lgn) * cn, 即θ(nlgn)
空间方面：Auxiliary Space: O(n)

Merge Sort vs Insertion Sort

虽然 Merge Sort 花费 O(nlgn) 时间，而 Insertion Sort 花费 O(n^2)
但在常数 c 上两者还是有很大区别的
事实上，在 Python 中，Merge Sort Running Time：2.2 nlgn
Insertion Sort Running Time: 0.2n^2
可见，当 n 较小时，用 Insertion Sort 是比较好的选择

谢谢你请我吃糖果：）